Rosebushes and cherry-trees -- and the Three Grices
This is rather a commentary on Jones's post on "Ontology and Metaphysics" (or "Metaphysics and Ontology") for which my thanks.
---
Jones writes:
"We are discussing infinity, and the views of Frege, Russell, Hilbert, Carnap and of course Grice.
And even Friedman."
Indeed. My focus should be on the symbolic terms for this:
Namely:
"∞" and
"ℵ0"
for, alla Grice, I would like to see how much of this can be incorporated into what Grice calls "System Q", and Myro called "System G", and Jones and I have called "System GHP (a hopefully plausible extension of Myro's System G -- or 'highly powerful', if you wish).
Our trigger has been Grice himself (to Strawson):
"If you cannot put it in symbols, it is not worth saying"
(with Strawson's rude retort omitted)
Jones goes on:
"I was thoroughly shocked by what JL culled from the Wikipedia entry on "Finitism" and to this I will shortly respond,"
"Shock" is the right word. We call it a "Wikipedia Shock". It relates to the fact that Wikipedia entries, like English folksongs, are ANONYMOUS (if not traditional). ("Folksongs -- I don't know why you call them so. Surely I never heard a horse singing one").
Jones goes on:
"but first I must correct an aspect of my previous posting, in which I described Carnap's move from Universalism to Pluralism as a movement from abstract to concrete."
Good. Indeed, I was led to think, when reading about "ABSTRACT", that we are dealing with things like propositions, intensions, and perhaps universals -- like properties. So I'm glad a consideration on this is due
Jones notes:
"Since the universalisms of Frege and Russell were both ontologically not entirely abstract this was not a good move (on my part)."
It may do to re-analyse what we mean by 'abstract' in different collocations: 'abstract entities' is perhaps what people like Grice are thinking of. Cfr. his critique of the 'bête noire' of Extensionalism (versus his favoured Intensionalism).
Jones notes:
"The terminology differs from one philosopher to another, but in Frege a relevant distinction is between concept and object, and Frege's logicism involved taking numbers (and generally extensions of concepts) as objects, which he later seems to have thought a mistake."
Good point.
Strictly, of course, the distinction should be between 'object' and 'subject', but let the Germans use the words more freely!
Jones goes on:
"In Russell, we have "individuals" rather than objects, and these do not include numbers (they are more concrete than that perhaps)"
Yes, 'individual' has the right Russellian ring to it, and I'm surprised that Strawson (in his "Individuals: an essay in descriptive metaphysics") does not dwell on the Russellian heritage
Jones:
".. but arithmetic does depend on there being infinitely many of them, which Russell, despite being a logicist regarded as contingent"
or even accidental!
Jones goes on:
"A better way of describing Carnap's move, which does fit into the way which he talks of it, is from the analytic to the synthetic."
Good point. The good old dogma (or underdogma, in Grandy's joke) in whose defense one could always count Grice to rally. (Grice/Strawson, "In defense of a dogma" -- the dogma of the analytic versus the synthetic) -- infamously and to some unconvincingly demolished by Quine
Jones goes on:
"For Carnap (though both Frege and Russell had their doubts), the Universalistic systems of Frege and Russell were both entirely analytic (which entails, for Carnap, consisting entirely of logical truths, in his "broad sense") and so therefore must be any claims obtained in those systems by the approved method of adding definitions and working within the same deductive system."
Good point. This connects with the early Wittgenstein (via Ramsey's logicism) and his view of logic and mathematics as tautological (a point taken up by Oxford's enfant terrible during Grice's early Oxford days: Ayer in his "Language, Truth and Logic".
Jones goes on:
"So to formalise empirical sciences (involving synthetic claims) Carnap adopts Hilbert's idea of deductive systems (rules and axioms) as providing implicit definitions of the ontologies they describe, aided and abetted perhaps by Hilbert's view that consistency suffices to establish existence (though I suppose this is irrelvant for Carnap who would. at least by the time of "Semantics and Empiricism", regard this doctrine as puporting to settle meaningless "external " questions)."
Good point. Carnap's view may connect with the idea of the "Unified Science" of the early positivists, and the sophisticated (or is it naive?) philosophy of science it endorsed. The idea that biology, for example, relies, like mathematics, on axioms, and rules of inference, and that the 'syntax' of all science should be uniform.
Jones goes on:
"The distinction between analytic and synthetic then derives from classifying rules and axioms into two groups, one [group of rules and axioms] determin[ing] meanings (and on the basis of which analyticity is determined), the other group [of rules and axioms -- or principles] expressing physical laws."
-- or regularities. I would go on to qualify this: a symbolic treatment of biology should deliver 'biological laws', a symbolic approach to sociology, 'sociological laws', and so on.
Jones goes on:
"A synthetic truth is then one which is determined by the rules and axioms altogether but not by the _logical_ rules and axioms alone."
Indeed. And perhaps it's 'principle' rather than 'axiom' that scientists in the different fields prefer to use.
It may do to revise the Greek history of this. The 'arkhe' versus the 'axiom'.
The Liddell and Scott ("I don't give a damn what the dictionary says!" -- Grice) dictionary of Greek gives for 'axioma':
A.
1.
that of which one is thought worthy, an honour,
“γάμων . . ἀξίωμ᾽ ἐδέξατο” E.Ion62; οἳ τὰς πόλεις ἔχουσι κἀξιώματαib. 605; “κοινῆς τραπέζης ἀ. ἔχειν” Id.Or.9; τὸ τῆς πόλεως ἀ. the dignity of the city's representative, D.18.149.
2. honour, reputation,
E.Supp. 424, Th.2.65, etc.; “ὢν ἐν ἀξιώματι ὑπὸ τῶν ἀστῶν” Id.6.15; “τὸ τῶν ἐλευθέρων γυναικῶν ἀ.” D.59.113: c. gen. objecti, ἀ. ἔχειν ἀρετῆς claim on ground of merit, Arist.Pol.1281b25.
5. concrete, things of dignity, Philostr.VS2.5.4.
II. that which is thought fit, decision, decree, “δαιμόνων” S.OC1452, cf. 1459; “τὰ τῶν προγόνων ἀ.” D.18.210; “ἀ. κενὰ καὶ νομοθεσίαι” Epicur.Ep.2p.36U.
2. in Science,
------
that which is assumed as the basis of
demonstration, self-evident principle.
Quotes:
—In Mathematics, axiom,
Arist.Metaph.1005a20, etc.
Philosophical doctrine, τὸ Ζήνωνος ἀ. ib.1001b7, cf. Xen.979b22; logical proposition, Chrysipp.Stoic.2.53,63, etc.
-----
We should expect the entry for 'arkhe' to be more confusing. But it is interesting that the basis for 'axioma' is in the 'axis' of 'axiology', hence the idea of what is 'valuable'. Note the uses in 'Science' and Mathematics. Liddell and Scott, typically, define the Greek 'axioma' as the English 'axiom', which is hardly illuminating -- but there's a crosslinguistic dictionary forya.
Suffice for now one expansion on Greek 'arkhe':
2. first principle, element, first so used by Anaximander, acc. to Simp. in Ph.150.23.
C
f. Arist. Metaph.983b11, etc.;
“Ἡράκλειτος τὴν ἀ. εἶναί φησι ψυχήν” Id.de An.405a25; of ὕλη and θεός, opp. στοιχεῖα, Placit.1.3.25; practical principle of conduct, “τῶν πράξεων τὰς ἀρχὰς καὶ τὰς ὑποθέσεις” D. 2.10;
principles of knowledge, Arist.Metaph.995b8, al.
-----
Jones goeson:
"With this amendment let me now move to the apparent relevance of the Wikipedia article on "Finitism" which JL has brought to our attention. The two startling revelations which JL pulls out of this are that both Hilbert and Friedman were finitists."
Indeed.
"With both of these I must take issue."
Note indeed that I provided the Hilbert reference in view of Jones's having mentioned him. The less developed reference to Friedman went as follows, for the record:
"By Harvey Friedman's grand conjecture most mathematical results should be provable using finitistic means."
Jones now expands on this.
Incidentally, the conjecture, as per Wikipedia
http://en.wikipedia.org/wiki/Elementary_function_arithmetic
reads:
Every theorem published in the Annals of Mathematics whose statement involves only finitary mathematical objects (i.e., what logicians call an arithmetical statement) can be proved in EFA.
EFA is the weak fragment of Peano Arithmetic based on the usual quantifier-free axioms for 0, 1, +, ×, exp, together with the scheme of induction for all formulas in the language all of whose quantifiers are bounded.
-----
Jones writes:
"Let us take Hilbert first. The purpose of Hilbert's "programme" was to save mathematics in the broadest sense, including "Cantor's paradise", from the intuitionists. [Hilbert's] idea was to defend mathematics involving so called ideal elements by obtaining a "finitary" proof of its consistency.
Hilbert was NOT himself a finitist."
Rather, Hilbet "sought a consistency proof for non-finitary mathematics which would be acceptable to finitists (though presumably a dyed-in-the-wool finitist would, after accepting the proof of consistency, still reject the formal system as "not mathematics")."
"What the Wikipedia article says about Hilbert seems to be unobjectionable but JL takes matters a step too far when he infers from it that Hilbert was a finitist."
Thanks for the caveat. I was misled indeed by the Wikipedia wording,
Under the section on "History" (of Finitism), the author states that "the introduction of infinite mathematical objects was a development in mathematics which occurred a few centuries ago."
"The use of infinite objects was a controversial topic among mathematicians."
"The issue entered a new phase when Georg Cantor, starting in 1874, introduced what is now called naive set theory and used it as a base for his work on transfinite numbers. When paradoxes such as Russell's paradox, Berry's paradox and the Burali-Forti paradox were discovered in Cantor's naive set theory, the issue became a heated topic among mathematicians."
"There were various positions taken by mathematicians."
"All agreed about finite mathematical objects like natural numbers. However there were disagreements regarding infinite mathematical objects. One position was the intuitionistic mathematics which was advocated by L.E.J. Brouwer which rejected the existence of infinite objects until they are constructed."
"Another position was endorsed by David Hilbert" -- and the rest is misinterpretation on my part! Sorry about that.
Jones then notes:
"When it comes to Friedman, my gripe is with Wikipedia. Friedman has devoted an extraordinary amount of talent and energy to showing that there are interesting parts of mathematics (inventing a whole new branch of mathematics in the process) which demand large cardinal axioms, hence going well beyond the ontological extravagances known to Cantor and Hilbert. Friedman might therefore be said to be an uber-infinitist"
-- label which I love of course!
----
INTERLUDE on the uber-Griceianism:
One of the first popular modern uses of the word"uber" as a synonym in English for super was a Saturday Night Live TV sketch in 1979.
The sketch, What if?, pondered the notion of what if the comic book hero Superman had landed in Nazi Germany when he first came from Krypton.
Rather than being called Superman, he took the name of Überman.
The term was also used in an episode of Friends (season 1, episode 5, "The One with the East German Laundry Detergent"), when Ross tries to impress Rachel by showing her that he uses a German laundry detergent called "Überweiss".
In the Philippines, a reality show franchise called Pinoy Big Brother has a segment show called Über that features extra scenes and discussions about the house-mates and provides edited and comical footage.
In the 2002 animated movie "Ice Age" Manfred the mammoth refers to Diego the sabre tooth cat as
"uber-tracker"
as they hunt the lone parent of the human baby that the trio has adopted.
Quote: "Hey, über-tracker. Up front where I can see you."
In the 2002 movie The Time Machine, the chief of the Morlocks is called the
"Über-Morlock".
In the novel The Mark of Athena by Rick Riordan, the main character, Piper McLean, describes her pillows in her room at the Argo II as
"über-comfortable".
During the 2000s, über also became known as a synonym for super due to games and gamers using the word.
For example, in the game SSX Tricky, a tricky move is also known as an
"über-trick."
In the video game Team Fortress 2, a playable class called the Medic has a healing gun that can deploy an
"Übercharge"
on a teammate which renders both temporarily invulnerable.
One of his domination phrases is
"I am the Übermensch!".
In Tony Hawk's Pro Skater 4 of PS1, the
"Uber Score"
is the most difficult score to achieve.
In Toy Soldiers, one of the bosses is a giant tank called the "Uber Tank".
In Dead Space 2, chapter 14-15 has an unkillable enemy known as the
"Ubermorph".
In Season 7 of Buffy the Vampire Slayer, a deadlier and more powerful vampire is introduced, given the name
"Übervamp"
by the show's protagonist.
--- end of 'uber' interlude.
Jones goes on:
"In taking Friedman to be a finitist JL can claim to have been mislead by the Wikipedia article, which does give an inaccurate description of one of Harvey Friedman's claims."
Good, and for the record, I have, above, appended, again from Wikipedia (alas!?) the very formulation of the conjecture.
Wikipedia states, as re-cited by Jones:
"However, by Harvey Friedman's grand conjecture most mathematical results should be provable using finitistic means."
"--- which certainly makes him sound close to a finitist", Jones comments.
"But when we follow the link to the "grand conjecture"", Jones notes, "we find it quoted as"
"Every theorem published in the Annals of Mathematics whose statement involves only finitary mathematical objects (i.e., what logicians call an arithmetical statement) can be proved in EFA."
"EFA is the weak fragment of Peano Arithmetic based on the usual quantifier-free axioms for 0, 1, +, ×, exp, together with the scheme of induction for all formulas in the language all of whose quantifiers are bounded."
Jones interestingly notes:
"The qualification "whose statement involves only finitary mathematical objects" is crucial."
Thanks for that.
Jones expands on his clarifying exegesis:
"Friedman is not talking about MOST of mathematics He is just talking about most of (published) arithmetic"
Indeed. And I was rather taken aback by the (c) reference to "Annals of Mathematics". It inspired me for a Speranza Conjecture:
"Every philosophical claim published in the "Mind", whose symbolic statement involves only the notation of Principia Mathematica may be proved."
----
INTERLUDE ON "MIND" AND "PROCEEDINGS OF THE ARISTOTELIAN SOCIETY" (journals where Grice published).
----
"The Annals of Mathematics (abbreviated Ann. Math. or Ann. of Math.) is a bimonthly mathematical journal published by Princeton University and the Institute for Advanced Study. It ranks amongst the most prestigious mathematics journals in the world by criteria such as impact factor."
"Mind" and "Proceedings of the Aristotelian Society" are the most prestigious publications in England.
"The journal began as The Analyst in 1874 and was established and edited by Joel E. Hendricks."
On the other hand, "Mind" began as a journal of psychology and philosophy. Hence the name.
On the other hand, the Aristotelian Society was always connected with the University of London.
The "Annals of Mathematics" was "intended to afford a medium for the presentation and analysis of any and all questions of interest or importance in pure and applied Mathematics, embracing especially all new and interesting discoveries in theoretical and practical astronomy, mechanical philosophy, and engineering". It was published in Des Moines, Iowa, and was the earliest American mathematics journal to be published continuously for more than a year or two. This incarnation of the journal ceased publication after its tenth year, in 1883, giving as an explanation Hendricks' declining health, but Hendricks made arrangements to have it taken over by new management, and it was continued from March 1884 as the Annals of Mathematics. The new incarnation of the journal was edited by Ormond Stone (University of Virginia). It moved to Harvard in 1899 before reaching its current home in Princeton in 1911. An important period for the journal was 1928–1958 with Solomon Lefschetz as editor. During this time, the annals became an increasingly well-known and respected journal. Its rise, in turn, stimulated American mathematics. Norman Steenrod characterized Lefschetz' impact as editor as follows: "The importance to American mathematicians of a first-class journal is that it sets high standards for them to aim at. In this somewhat indirect manner, Lefschetz profoundly affected the development of mathematics in the United States."[9]
Princeton University continued to publish the annals on its own until 1933, when the Institute for Advanced Study took joint editorial control. Since 1998 it has been available in an electronic edition, alongside its regular print edition. The electronic edition was available without charge, as an open access journal, but since 2008 this is no longer the case. Editions before 2003 were transferred to the non-free JSTOR archive, and articles are not freely available until 5 years after publication.
The current editors of the Annals of Mathematics are Jean Bourgain, Richard Taylor (both from the Institute for Advanced Study), David Gabai, Nick Katz, Sergiu Klainerman, and Gang Tian (all from Princeton University).[10]
According to the Journal Citation Reports, the journal has a 2009 impact factor of 4.174, ranking it first among 255 journals in the category "Mathematics".
--- end of expansive note on "Annals of Mahtematics" reference by Friedmann.
Jones goes on:
"None of this is terribly important to the matters under discussion, but my suggestion that Carnap's pluralism was partly inspired by Hilbert makes no sense unless we understand Hilbert as ontologically liberal."
Understood. Thanks about that.
Hilbert is/was a genius, in having been so influential in so many respects, then.
His major influence on me was his quote:
"If I were to awaken after having slept for a thousand years,
my first question would be: Has the Riemann hypothesis been proven?"
----
Another favourite Hilbert quote of mine, involves the obvious negative:
"I do not see that the sex of the candidate is an argument against her admission as a Privatdozent. After all, the Senate is not a bath-house."
-----
And one that may have a Griceian resonance to it:
Hilbert:
"Every kind of science, if it has only reached a certain degree of maturity, automatically becomes a part of mathematics".
- Axiomatic Thought (1918), printed in from Kant to Hilbert, Vol. 2 by Ewald
---- In the case of Grice, the importance of 'implicature' connects. Because it is only when grasping the 'logical form' in terms of symbolic notation that we can expand on what this form IMPLICATES rather than says or expresses.
Another quote by Hilbert touches on the 'finite':
Hilbert:
"It remains to discuss briefly what general requirements may be justly laid down for the solution of a mathematical problem."
"I should say first of all, this: that it shall be possible to establish the correctness of the solution by means of a FINITE number of steps based upon a FINITE number of hypotheses which are implied in the statement of the problem and which must always be exactly formulated."
"This requirement of logical deduction by means of a FINITE number of processes is simply the requirement of rigour in reasoning."
---
INTERLUDE On Hilbert's life:
"Hilbert remained at the University of Königsberg as a Privatdozent (senior lecturer) from 1886 to 1895."
"In 1892, Hilbert married Käthe Jerosch (1864–1945), "the daughter of a Konigsberg merchant, an outspoken young lady with an independence of mind that matched his own"".
"While at Königsberg they had their one child, Franz Hilbert (1893–1969)."
"In 1895, as a result of intervention on his behalf by Felix Klein, he obtained the position of Professor of Mathematics at the University of Göttingen, at that time the best research center for mathematics in the world. He remained there for the rest of his life."
"His son Franz suffered throughout his life from an undiagnosed mental illness: his inferior intellect was a terrible disappointment to his father and this misfortune was a matter of distress to the mathematicians and students at Göttingen."
--end of Hilbert interlude
Jones goes on:
"Carnap's ontological position is, so far as I know, original and a substantial departure from precedent, even in positivist circles."
"Kolakowski identifies four key features of positivist philosophy one of which is "nominalism"".
"In Carnap we find an abhorrence of "metaphysics" (though this may not be in Carnap what you might have thought), and though one might have expected nominalism to flow from this, Carnap's conception of metaphysics
***rejects nominalism**** no less than platonism."
Interesting to know
Jones:
"Carnap tells us that the negation of a metaphysical claim is also metaphysical, and that we can distinguish ontological claims according to whether they are made in the context of some conventional ontology, and hence may be established or refuted using those conventions, or are made in vacuo and are then meaningless and no more refutable than confirmable. The resulting ontological liberalism is not dissimilar to that which we seem to find in Grice, though in Grice I am not aware of a comparably incisive philosophical underpinning."
Indeed. Grice thought he should complete a whole treatise on metaphysics. He went on to entitle it, "From Genesis to Revelations" -- being a new discourse on metaphysics. It remains mainly in bits and pieces in his unpublications.
He ended up his 'metaphysician' career as defending, against Strawson, 'revisionary', rather than 'descriptive' metaphysics.
-----
Jones:
"It seems to me also that it is more in touch with the workings of ordinary language than philosophy generally has been, for it surely is the case that most ordinary ontological discourse belongs to some context which more or less determines the ontological criteria involved."
Indeed. Grice used the simile of 'landscapes' here -- and he would often refer to the landscape of England!
A favourite quote of mine being:
"In favour of minimalism, we might hear, an appeal, echoing
Quine, to the beauty of 'desert landscapes'."
"But," Grice hastens to add, "such an appeal I would regard as inappropriate; we are not being
asked by a Minimalist to give our vote to a special, and no
doubt very fine, type of landscape."
--- cfr. Hart and Strawson's review of Quine: "A logician's landscape".
"We are being asked," Grice notes, "to express our preference for an ordinary sort of lanscape, to
rosebushes and cherry-trees in midwinter, rather than in
spring or summer."
Grice's reaction:
"To change the image somewhat, what bothers me about what I'm being offered is not that it is
bare, but that it has been systematically and relentlessly
_undressed_"
Grice, "The Life and Opinions of Paul Grice",
in PGRICE, ed. Grandy/Warner, Philosophical Grounds of Rationality: Intentions, Categories, Ends, p. 68.
A permanent interest in Grice was the concern of metaphysics as providing the general categorial framework, realised indeed in the 'vernacular' -- his inquisition on a 'linguistic' versus an 'ontological' category.
Jones goes on:
"Going back to the stars and their infinity, it seems to me that, in ordinary language, to talk of the infinity of stars may have a meaning quite different to that which either a mathematician or a physicist might assign to it."
Indeed. Note that as Russell would have it, we need to distinguish between what he called, rather old-fashionedly now, "Twentieth-century physics". Russell contrasted this with "Stone-Age Metaphysics". Grice was offended by the remark by Grice, and would often use "Stone-Age PHYSICS", instead.
Jones:
"and be compatible with presently received opinion among cosmologists."
Perhaps I should double check with Wikipedia on 'stars'!
On the other hand, there's the lyric:
http://lyrics.wikia.com/Kelli_Ali:The_Infinite_Stars
In your arms, the infinite stars
Collide and come together
Blue blue days
Without you
I spend in disarray
If the world is goin' to end
Then I'd feel so much better
If you love love love me
Hey hey hey
The Wikipedia entry for 'universe' reads:
"The size of the Universe is unknown; it may be infinite."
But then again it may not.
There is a reason to this indeterminacy:
"Since we cannot observe space beyond the limitations of light (or any electromagnetic radiation)", the Wikipedia states, "it is uncertain whether the size of the Universe is finite or infinite."
"Aristotle developed the notion of a potential countable infinity, as well as the infinitely divisible continuum."
"Unlike the eternal and unchanging cycles of time, Aristotle believed the world was bounded by the celestial spheres, and thus magnitude was only FINITELY multiplicative."
"Borrowing from Aristotle's Physics and Metaphysics, philosophers have employed two logical arguments against an infinite past, the first being the "argument from the impossibility of the existence of an actual infinite", which states as follows."
"An actual infinite cannot exist."
"An infinite temporal regress of events is an actual infinite."
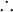An infinite temporal regress of events cannot exist."The second argument, the "argument from the impossibility of completing an actual infinite by successive addition", states.
"An actual infinite cannot be completed by successive addition."
"The temporal series of past events has been completed by successive addition."
"
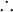The temporal series of past events cannot be an actual infinite."Edmund Halley (1720) and Jean-Philippe de Cheseaux (1744) noted independently that the assumption of an infinite space filled uniformly with [Grice's lucky] stars would lead to the prediction that the night-time sky would be as bright as the sun itself.
This became known as Olbers' paradox in the 19th century.
----
Newton (who worked in Lincolnshire? -- genius) believed that an infinite space uniformly filled with matter would cause infinite forces and instabilities causing the matter to be crushed inwards under its own gravity.
This instability was clarified in 1902 by the Jeans instability criterion.
|
Space has no
boundary – that is empirically more certain than any external
observation. However, that does not imply that space is infinite.
|
|
Bernhard Riemann (Habilitationsvortrag, 1854)
|
"If k is zero or negative, the Universe may have infinite volume, depending on its overall topology."
"It may seem counter-intuitive that an infinite and yet infinitely dense Universe could be created in a single instant at the Big Bang when R=0, but exactly that is predicted mathematically when k does not equal 1."
"For comparison, an infinite plane has zero curvature but infinite area, whereas an infinite cylinder is finite in one direction and a torus is finite in both."
Jones goes on:
"It is arguable that the claim asserts no more than that the stars are so numerous that there is no practical possibility of counting their number."
Indeed. It may be just hyperbolic. Alas, Grice's other example of an hyperbole does not help us here:
"Every nice girl loves a sailor" ("Hyperbole as conversational implicature", in Way of Words).
One point to consider is the use of 'infinite' as an adverb: "infinitely many", since, after all, as they say, infinite is NOT a number.
The logic of 'many' belongs in a separate branch of logic (pleonetetics) as developed by Altham.
----
Jones concludes his interesting note:
"There may be even in the pedestrian assertion something like the poetic licence which allows us to talk of infinite sorrow, joy, beauty."
Indeed, and I have indeed illustrated a dictum by Marlowe, which relates:
http://home.cc.gatech.edu/je77/118
Had I as many souls as there be stars, I'd give them all for Mephistopheles. By him I'll be great Emperor of the world, And make a bridge through the moving air, To pass the ocean with a band of men; I'll join the hills that bind the Afric shore, And make that continent to Spain, And both contributory to my crown. The Emperor shall not live but by my leave, Nor any potentate of fair Europe. Now that I have obtain'd what I desire, I'll live in speculation of this art Till Mephistopheles return again.
Conversational application:
Grice: As far as I know, there are infinitely many stars.
Strawson: As far as you don't know, you surely mean.
Grice: Hmpf.
----
Fausto: Had I as many souls as there be stars I'd give them all for Mephistopheles.
Margherita: What do you mean, 'as many'? How many stars _are_ you saying there are?
Fausto: Surely infinitely many.
Margherita: Then I guess I could prove, alla Hilbert, since the act of giving, like that of proving, should involve a finite sequence of steps, you better wish the number of stars is FINITE?
Fausto: Hmpf and double hmpf.
Posts
No comments:
Post a Comment