Speranza
This is a commentary on Jones's post with this name.
Jones writes:
"Rather than just picking holes in Speranza's posts on infinity I thought I
should say something more constructive. Speranza raised the question how
one would add an axiom of infinity into Grice's formal treatments relating to
vacuous names, so I had a look back at my rehash of this material to see how
that might work. Before coming to Grice it's worth pointing out some
different kinds of axiom of infinity."
Good point. Variants:
different kinds of axiom of infinity.
different axioms of infinity
different axioms of infinities!
---- A transfinitist should not be surprised if the variants on the axioms of infinity turn to be transfinite.
Jones goes on:
"Speranza [first] discussed infinity in
connection with "finitism", and the definition of a finitist (at Wikipedia) is
"only accepts the existence of FINITE mathematical objects". This means that
the axiom of infinity in NBG which Speranza discussed would NOT be acceptable to
a finitist."
Good point. Yet it looks SO ELEGANT, that one is starting to doubt as to canons of elegance on the part of finitists.
Jones goes on:
""The" axiom of infinity also arises in the context of Russell
and Whitehead's Principia Mathematica.
To do arithematic in Russell's Theory
of Types you need an axiom of infinity, and it is a curiosity that Russell
remained a logicist even though he considered the axiom of infinity used in
Principia to be contingent."
Excellent point. THIS is a connection to consider seriously. For, if we re-read Grice's "Retrospective Epilogue" (written in 1987, for the reprint of his essays in "Studies in the Way of Words") we see that he defines things in two groups:
-- the classicists or heirs to "Principia Mathematica" (like himself)
-- the 'neo-traditionalists' -- like Strawson.
(It is interesting to reconsider this in the Oxonian context, and also in terms of those who studied IN the Oxonian context: R. Read, for example, student of Hacker and Baker -- and the point being made that Strawson, for example, with his endorsement of ordinary-language was an "Oxonian Wittgensteinian" -- On the other hand, Grice certainly favoured a canonical notation to make his points about, say, implicature, ever more obvious -- "What you cannot formalise is not worth saying")
Note that Grice calls Strawson a 'neo-traditionalist', i.e. a traditionalist that is reacting to the classicism of the 'modernists' who feel they are heirs to Principia Mathematica.
---
(It may be argued that strictly Grice is not a modernist, but what I once called a 'post-modern', in that he must take into account, at least, the observations by Strawson, even if to provide a reply which is consistent with the canons of modernism or classicism alla Principia Mathematica -- this interpretation of Grice as 'post-modern' is consistent with his remarks, made often, that he had 'one foot in each camp' or that he fell that both modernists and neo-traditionalists were victims of 'a same mistake' -- to disregard the nature of conversation and how it operates -- notably constraints like informativeness in semantic content that gets explicitly represented).
Jones goes on:
"The need of an axiom of infinity (or something
equivalent) for doing arithmetic, is not peculiar to Russell's Theory of Types,
is it common to all treatments of arithmetic including those approved by
finitists (such as PRA), so how can this be if finitists reject the axiom of
infinity? The answer is that there are two quite different things which
an axiom of infinity might do."
Very good point. For one surely takes for granted that axioms can't do much other than _be_ axioms.
Jones:
"In the case of ZFC, NBG and most set theories,
the axiom of infinity asserts the existence of a set with infinitely many
elements. To do arithemetic we do need infinitely many numbers"
whereas, obviously, to use Grice's example in Way of Words, to do cosmology we do NOT need 'infinitely many stars'.
Jones goes on:
"... but we don't
necessarily have to have them collected together into a set. In PA and in
PRA, and in most first-order formalisations of arithmetic, you have an axiom of
infinity or its equivalent, but you don't have any infinite objects."
Very good point. And this connects, I hope, with our former discussion of a Frege-type ontology of concepts and objects or in Russellian parlance, 'individuals'.
Jones goes on:
"In fact,
the Peano axioms can be read as a way of asserting that there are infintely many
things."
Indeed, and this is good way to reminisce the man, who created so much useful formalism, into the bargain!
Jones:
"These give us ANOTHER general formula for asserting that there
are infinitely many things [like numbers of stars] which does not require the existence of sets. We
assert the existence of a distinguished element (think "zero") and a one-one
function (think "successor") such that the distinguished element is not in the
range of the function ("zero" is not a "successor")."
Very clear. Thanks.
Jones:
"This ensures that if, as we
count from the distinguished element ("zero") using the function to increment, we get a
new object every time, and count our way through an infinity of objects
(numbers)."
It may be different with stars.
But then, I am reminded of the phrase, "From zero to infinity", which allows me to introduce an INTERLUDE, here, from:
http://en.wikiversity.org/wiki/Zero_unity_and_infinity,
entitled,
"Zero, Unity and Infinity."
Zero signifies a place holder that is empty. Unity signifies existant object. Infinity signifies multitude.
The definitions are not each of the same order, since the nature of the matter is not understandable without Q.
Q signifies the quantum indefinite.
For this reason, the matter of this discourse will be presented in a manner consistent with its own nature, which is non-linear.
Each definition will be provided in a simplest possible term to start with, and then as required each definition will be expanded in order to clarify the understanding that is developed.
1.1=1
0.0=0
∞.∞ = ∞
If a.b=c then c/a=b and c/b=a
If 1.1=1 then 1/1=1
If 0.0=0 then 0/0=0
If ∞.∞ = ∞ then ∞/∞ = ∞
But:
If 1.∞=∞ then that means ∞/∞=1 and ∞/1=∞
Therefore infinity divided by infinity gives either unity or infinity, but it does not give zero.
And:
If 0.∞=0 then that means 0/0=∞ and 0/∞=0
Therefore zero divided by zero gives either zero or infinity, but it does not give unity.
And:
If 1.0=0 then that means 0/1=0 and 0/0=1
Therefore zero divided by zero gives unity and zero divided by unity gives zero, but neither answer gives infinity.
However that means zero divided by zero gives three possible answers, that is infinity, unity or zero.
And infinity divided by infinity gives two possible answers, that is infinity or unity. And unity divided by unity gives one possible answer, that is unity.
For information as to a related matter see:
http://en.wikiversity.org/wiki/Geometria
The basic equation of modern physics is f=ma. Force is equal to mass multiplied by acceleration.
The equation f=ma is dependent on the earlier structure:
If a.b=c then c/a=b and c/b=a
This point is quite difficult to grasp if it is the first time of considering the matter, and many physicists who completely understand the fundamental equation of modern physics, do not necessarily understand the more fundamental matter on which the equation rests.
Only if it is true that: If a.b=c then c/a=b and c/b=a
Then may it be true that: If m.a=f and f/m=a and f/a=m
Therefore, the point that I would like to make clear here is that a more fundamental subject exists of which the equation:
a.b=c then c/a=b and c/b=a
is one example of that more fundamental subject.
The reason that the matter has to be clarified in this sort of way is because the fabric of the subject is not so obvious to the enquirer. So whereas we can immediately comprehend the importance of such a prestigious equation as f=ma, the fact that such a prestigious equation is based on some other thing does not immediately hold the attention.
First statement:
a means "a is true" Affirmation. Or "a" means an entity in the universe of discourse that may be a genus or species, or may be a class or member of class, or may be a set or element of set.Or "a" means everything that is "a" in our universe of discourse.
~a means "a is false" Negation. Or "~a" means everything that is "not a" in the universe of discourse. Or "~a" means some entity that is an element of everything that is not "a" in the universe of discourse.
b means "b is true" Affirmation. Or some entity not a in the universe of discourse that may be defined in a similar manner to the way in which a is defined.
~b means "b is false" Negation. Or some entity not b in the universe of discourse that may be defined in relation to b in a similar manner to the way in which not a is defined in relation to a.
a v b means "either a is true, or b is true, or both" Either one or the other or both.
a ^ b means "both a and b are true" And. Both one and the other.
a => b means "if a is true, then b is true". If - then. If set of elements then any element of such a set.
a =/=> b means "if a is true, then b is false". If - then not . If set of elements then not any element of a different set.
a < b means "since b is true, then a is true." Since - then. Since the way this system uses the inclusion sign label may be inconsistent with the way other systems use the same sign label it requires further clarification. My definition is as follows: (a < b) ^ (b < c) => a < c. That is to say, if a contains b, and b contains c, then a contains c. I am using the sign label as an arrow to show that the species is part of the genus or that the element is contained by the set.
a /< b means "since b is true, then a is false." Since - not then. If member of a class, then not any different class.
a <=> b means "a and b are either both true or both false" If and only if. Only if both and not either one without the other.
a <=/=> b means "a is true and b is false, or a is false and b is true". Either one or the other not both.
ɸ means the empty set, or the class whose membership is none.
1 means the unity set, or the class whose membership is itself.
e means everything in the given universe of discourse.
! means not not. Or in regard to a single entity it means neither entity nor not entity.
Q means neither the unity set nor the empty set. Or an indefinite variable.
Second statement:
ʘ means the universal abstraction. ʘ => ʒ ^ e The universal abstraction is the universe of discourse and everything in it.
ψ means the universal operator. ψa => a ^ ~a ^ !a The universal operator is every and all of some possible entity.
Э means the existential operator. Эa => a v ~a v !a The existential operator is some possible entity of all such entity.
ʒ means the universe of discourse. ʒ => e The universe of discourse is a restricted parameter bounded by the terms of meaning.
ɸ means the empty set. ɸ => ʒ ^ ~e The empty set is the class whose membership is none or the set of no elements.
1 means the unity set. 1 => a < a The unity set is the class whose membership is itself or the set that contains itself as element.
e means everything in the universe of discourse. e => a ^ ~a Everything in the universe of discourse is only and all the sign labels used.
Q means not the empty set and not the unity set. Q => ~ɸ ^ ~1 Not the empty set and not the unity set is the indefinite variable or possible improbable.
! means not not entity. !a => ~(~a) Not not entity is neither entity nor not entity.
Third statement:
46. ʘ => ʒ ^ e
47. ψa => a ^ ~a ^ !a
48. Эa => a v ~a v !a
49. ʒ => e
50. ɸ => ʒ ^ ~e
51. 1 => a < a
52. e => a ^ ~a
53. Q => ~ɸ ^ ~1
54. !a => ~(~a)
55. ʘ => ʒ ^ e < (Q ^ !e) v [(ɸ ^ 1) ^ (ψ ^ Э)]
Fourth statement:
zi': ɸ ^ ɸ => ɸ zi": ɸ ^ ~ɸ => Q zi"': ɸ v ɸ => ɸ zi"": ɸ < ɸ => ∞
zii': ɸ v 1 => ɸ zii": 1 v ɸ => ɸ zii"': ɸ < 1 => ɸ zii"": 1 < ɸ => ɸ
ziii': ɸ v a => ɸ ziii": a v ɸ => ɸ ziii"': ɸ < a => ɸ ziii"": a < ɸ => ɸ
ziv': ɸ v ~a => ɸ ziv": ~a v ɸ => ɸ ziv"': ɸ < ~a => ɸ ziv"": ~a < ɸ => ɸ
zv': 1 ^ ~1 => Q zv": a ^ ~a => e zv"': ~a ^ ~(~a) => !ɸ zv"": a ^ ~a => e
Fifth statement:
1. a => a If a, then a.
2. ~a => ~a If not a, then not a.
3. a =/=> ~a If a, then not not a.
4. a ^ ɸ => a If a and the empty set, then a.
5. a ^ ~ɸ => a If a and not the empty set, then a.
6. ~a ^ ɸ => ~a If not a and the empty set, then not a.
7. ~a ^ ~ɸ => ~a If not a and not the empty set, then not a.
8. a v 1 => a If a or the unity set, then a.
9. a < 1 => a If a includes the unity set, then a.
10. ~a v 1 => ~a If not a or the unity set, then not a.
11. ~a < 1 => ~a If not a includes the unity set, then not a.
12. a v ɸ => ɸ If a or the empty set, then the empty set.
13. a < ɸ => ɸ If a includes the empty set, then the empty set.
14. ~a v ɸ => ɸ If not a or the empty set, then the empty set.
15. ~a < ɸ => ɸ If not a includes the empty set, then the empty set.
16. a ^ 1 => 1 ^ a If a and the unity set, then the unity set and a.
17. a ^ ~1 => Q ^ a If a and not the unity set, then Q and a.
18. ~a ^ 1 => 1 ^ ~a If not a and the unity set, then the unity set and not a.
19. ~a ^ ~1 => Q ^ ~a If not a and not the unity set, then Q and not a.
20. ɸ ^ a => a If the empty set and a, then a.
21. ɸ ^ ~a => ~a If the empty set and not a, then not a.
22. ɸ ^ ~(~a) => !a If the empty set and not not a, then !a.
23. a ^ a => a ^ a If a and a, then a and a.
24. a v a => a If a or a, then a.
25. a ^ ~a => e If a and not a, then everything in the universe of discourse.
26. a < a => 1 If a includes a, then the unity set.
27. a v ~a => Q If a or not a, then Q.
28. a ^ ~(~a) => a ^ !a If a and not not a, then a and !a.
29. a < ~(~a) => a < !a If a includes not not a, then a includes entity neither a nor not a.
30. a v b => b v a If a or b, then b or a.
31. a ^ b => b ^ a If a and b, then b and a.
32. (a ^ b) ^ c => a ^ (b ^ c) If term a and b term and c, then a and term b and c.
33. (a v b) v c => a v (b v c) If term a or b term or c, then a or term b or c.
34. a ^ (b v c) => (a ^ b) v (a ^ c) If a and term b or c, then term a and b term or term a and c.
35. a v (b ^ c) => (a v b) ^ (a v c) If a or term b and c, then term a or b term and term a or c.
36. ~(a ^ b) => ~a ^ ~b If not term a and b, then not a and not b.
37. ~(a v b) => ~a v ~b If not term a or b, then not a or not b.
38. a < b => a < b If a includes b, then a includes b.
39. a ^ ~b => ~b ^ a If a and not b, then not b and a.
40. (a ^ ~b) ^ ~c => a ^ (~b ^ ~c) If term a and not b term and not c, then a and term not b and not c.
41. (a < b) < c => a < (b < c) If term a includes b term includes c, then a includes term b includes c.
42. a ^ ~(b < c) => (a ^ ~b) < (a ^ ~c) If a and not term b inc c, then term a and not b term inc term a and not c.
43. a < (b ^ ~c) => (a < b) ^ ~(a < c) If a inc term b and not c, then term a inc b term and not term a inc c.
44. ~(a ^ ~b) => ~a ^ ~(~b) If not term a and not b, then not a and not not b.
45. ~(a < b) => ~a < ~b In not term a inc b, then not a inc not b.
Sixth statement:
The above ideas 1 through 45. Each idea the synthesis of individual concepts. The synthesis of ideas a notion. Correct as stated and if correctly stated then true or not. But then heuristic. Correct as stated or not, does not matter. At least we can see a complete notion. And we can see the forty five ideas that combine to provide the notion. And we see we have a small specific number of concepts to consider.
Take any one idea. Specify idea 26. It is easy to see that idea 26 is not correct as stated, since it is deliberately not giving all the possible correct answers. Idea 26 says a divided by a is unity. Which we can expand into word language to say that if a thing is contained by itself then the result is unity. But that is only true if a is a positive integer. The reason we say a/a=1 is because 1/1=1, 2/2=1, 3/3=1, so then a is any positive integer. But a could be a negative integer. Then a/a = 0 if any negative integer divided by itself is zero or a/a = b if any negative integer divided by itself is a different unknown variable not a. But a could be zero. Then a/a = ∞ if zero divided by zero is infinity. But then we would have to say Э∞ and not the ψ∞ . Therefore a / a = Э∞ which is the particular infinity made when the empty set contains itself, since it means a continuum of nothing containing nothing in an unlimited way.
Translated into sets is
a <=> ɸ, ^ ɸ < ɸ => Э∞ ^~ ψ∞, => a < a => Э∞ ^~ ψ∞.
Which says if and only if a is the empty set, and, the empty set containing the empty set is one species of infinity and not the genus of that type of infinity, then a containing a is one species of infinity and not the genus of that type of infinity.
And if "a <=> +n, ^ +n < +n => 1, => a < a => 1."
Which says if and only if a is a positive integer, where +n is any positive integer, then given any positive integer containing itself gives unity, if a containing a then unity.
And if "a <=> -n, ^ -n < -n => b, => a < a => b."
Which says if and only if a is a negative integer, where -n is any negative integer, then given any negative integer containing itself gives an unknown variable b, where b is any unknown variable, if a containing a then unknown variable b.
Therefore, the notion that can be developed from idea 26 is as follows:
26.i - "a <=> ɸ, ^ ɸ < ɸ => Э∞ ^~ ψ∞, => a < a => Э∞ ^~ ψ∞."
26.ii - "a <=> +n, ^ +n < +n => 1, => a < a => 1."
26.iii - "a <=> -n, ^ -n < -n => b, => a < a => b."
26.iv - "a/a = 1 or ∞ or b".
Seventh statement:
Quantum indefinite, neither entity nor not entity, existential operator, universal operator, everything in the universe of discourse, empty set, unity set, infinity.
The sixth statement offers a preferred line in terms of correction of any aspect of the ideas as stated.
The sense would be to not adjust any of the stated ideas one to forty five at the level they are stated.
But instead to take any one idea, each one after the other, in any order and specify idea ten, fifteen or thirty two or whatever. And then to challenge that one idea, either to show that it is false as stated, or that it is not entirely correct, or alternatively to prove that as stated it is entirely correct and true.
In doing so, one can prove using the language of the system as demonstrated for idea 26:
26.i - "a <=> ɸ, ^ ɸ < ɸ => Э∞ ^~ ψ∞, => a < a => Э∞ ^~ ψ∞."
26.ii - "a <=> +n, ^ +n < +n => 1, => a < a => 1."
26.iii - "a <=> -n, ^ -n < -n => b, => a < a => b."
26.iv - "a/a = 1 or ∞ or b".
In this way, if the original ideas are not adjusted at the level they are provided, then it will enable different decision makers the freedom to check the truth and correctness of the propositions, each from a common ground.
That will then mean that it is not necessary for two different decision makers to assign the same decision as to truth or falsity or neither true nor false to any one idea.
For a complete index to the various articles I have used to introduce these and related patterns, please follow the hyperlink:
http://en.wikiversity.org/wiki/Deductive_logic
------- END OF INTERLUDE.
Jones goes on:
"Sorry, it does here look like we have asserted the existence of a
"sucessor" function, which itself is an infinite "object," but though we make use of
the function, we don't actually ASSERT its existence"
perhaps we may just IMPLICATE it, as it were -- cfr.
"Marmaduke Bloggs was the greatest invention by journalists ever made"
or something.
---
Or
"If you believed in the existence of Marmaduke Bloggs, then you were misled by the Merseyside journalists", or something.
Of course, Jones's point is subtler. He is referring to the Frege sign:
⊦
-- so-called "assertion sign" -- I think Grice prefers 'alethic sign' -- in "Aspects of reason" -- and noticing that the 'successor function' need not occur in formulae involving that sign.
Jones goes on:
"... and it isn't in the range of our
quantifiers, so there is a bit of (logically coherent) fudge going on
here."
Must say I like this, since I think mathematicians should use fudge ever more often.
INTERLUDE ON HARDY'S MATHEMATICS as coherent fudge -- vide "The man who knew infinity".
fudge (n.)  type of confection, 1895, American English.Apparently a word first used among students at women's colleges.Perhaps a special use of fudge (v.). 'He lies,' answered Lord Etherington, 'so far as he pretends I know of such papers. I consider the whole story as froth -- foam, fudge, or whatever is most unsubstantial'[Scott, "St. Ronan's Well," 1823]
type of confection, 1895, American English.Apparently a word first used among students at women's colleges.Perhaps a special use of fudge (v.). 'He lies,' answered Lord Etherington, 'so far as he pretends I know of such papers. I consider the whole story as froth -- foam, fudge, or whatever is most unsubstantial'[Scott, "St. Ronan's Well," 1823]
-----
where 'unsubstantial' is the antonym of 'substantial' as used by Aristotle -- see Jones, "Aristotle's Metaphysics".
fudge (v.)  "put together clumsily or dishonestly," 1610s, perhaps an alteration of "fadge", make suit, fit" (1570s), of unknown origin. As an interjection meaning "lies, nonsense" from 1766.
"put together clumsily or dishonestly," 1610s, perhaps an alteration of "fadge", make suit, fit" (1570s), of unknown origin. As an interjection meaning "lies, nonsense" from 1766.
The noun meaning "nonsense" is 1791. ----- perhaps it should have been used by Carnap in his demolition of metaphysics, "Nothing noths", as uttered by Martin Heidegger being a bit of logically incoherent fudge. ---- "fudge" could be a natural extension from the verb, 'fudge'.
But Farmer suggests provincial French "
fuche,
feuche", which is an exclamation of contempt from Low German "
futsch", begone.
The traditional English story traces "
fudge" in THIS sense (but cfr. Grice, Do not multiply senses beyond necessity) to a sailor's retort to anything considered lies or nonsense, from
"Captain
Fudge",
who always brought home his owners a good cargo of lies"
Isaac Disraeli, 1791, citing a pamphlet from 1700.
It seems there REALLY WAS a late 17c. Captain Fudge
-- and so would not strictly qualify as one of Grice's Vacuous Names (cfr. Pegasus). He was called "Lying Fudge".
Perhaps his [non-vacuous] name reinforced this form of "
fadge" in the sense of "contrive without the necessary materials."
The surname is, incidentally, from "
Fuche", a pet form of the masculine proper name "
Fulcher," from Germanic and meaning literally "people-army."
------- END OF FUDGE interlude.
Jones goes on:
"Going back to Grice's formal systems and considering the question
how to introduce an axiom of infinity, there are therefore a number of choices
to be made."
Good. Grice would have liked that.
"The first is whether we just want there to be infinitely many
THINGS"
like stars, so that we can save ordinary language from self-contradictoriness, in statements that Grice explicitly consider when he says:
"As far as I know, there are infinitely many stars"
Jones goes on:
"... so that we could do arithmetic [and cosmology -- cfr. "Nostalgia for the stars" --- there are also a couple of interesting comments by Witters on this that may connect -- different post], or whether we want there to be things
with infinite extensions (so we don't get confounded with finitists, or perhaps
because we think that Ordinary Language is just as expressive as set
theory)."
This is an excellent point. For _I_ would start by tracing ALL (or most) expressions in Ordinary Language (say English) that COMMIT to the use of infinity (in its notational variants,
∞
א
in mottoes like
"never say never"
"always"
"endlessly"
--- and finitist variants, "till the end of time" (used by Connolly in recent film, "Quartet", as I recall -- "I'll love you till the end of time" -- implicature open).
Jones goes on:
"To do the former, we could just add in the Peano principles".
Good to know.
"To do
the latter, the language of sets and the assertion of a set closed under some
successor relationship will do."
Good to know, too.
"That was really the easy
question" -- with an excellently clarifying answer, too!
Jones goes on:
"Grice's system raised more DIFFICULT questions because it has
different notions of "existence" and so when we ASSERT the EXISTENCE of sets we
might (or might not) be doing something similar to asserting, "Pegasus flies " and hence, Grice insists, that somehow, "Pegasus exists."
Excellent point.
I especially adore the way Grice connects this with 'negation'.
"Marmaduke Bloggs doesn't exist"
"So, someone will not be at a party".
"Did you hear me clearly? I said he doesn't exist".
"So? I'm using "not".
----- But Jones's choice of "Pegasus" is more perspicuous. For a fuller treatment, I refer to Jones's pdf document on the topic, where he discusses the various notational variants, and the incidental reference by Grice to his system not creating 'ontological jungles' like Meinong's!
Jones goes on:
"So here is a
question about Grice for Speranza."
Mmm. Let's see.
Jones:
"When it comes to set theory in the
context of his treatment of 'Vacuous Names', would Grice be thinking of sets as
"logical fictions", and hence want to treat sets as non-denoting, or do we want
sets to be more solid than that?"
I'll think about that! It may do to revise what QUINE (of all people) thought of all this. Recall that his "Vacuous Names" was meant as a tribute to Quine (and properly printed in the book, "Words and ObjectIONS"). As I recall, Quine found all of Grice's paraphernalia merely decorative, and not dealing with abstract theoretical questions as whether sets are non-denoting.
----
Jones goes on:
"One issue which arises in this context is
whether one can pile fictions on top of each other in the way that sets can be
made from sets. Can on have a fiction which is build out of fictions in some
way?"
Perhaps Grice would not use 'fiction' (which is used by Bentham?), but 'construction'. Recall that his first essay ever (almost), "Personal identity", treats of sentences containing the ellusive "I" ("I was hit by a cricket bat," "I fell from the stairs", "I'm thinking of joining the army") in terms of an ordered set of mnenomic states.
Grice is VERY clear there (and later) that he was thinking of Broad's classification of approaches, and that HIS was one of a 'logical construction' (rather than logical fiction).
Jones:
"Is it consistent with Grice's system that not only do sets fail to
denote, but that their members lack denotations as well?"
Well, at this point, it may to to revise Austin, who was possibly Grice's precursor there. When Austin refers to things like 'meaning' he obviously has Frege in mind, with the distinction of 'sense' and reference (rather than 'denotation'). And so, Grice would be clearer as to what we mean 'refer'. Austin, as we know, distinguished three aspects:
the locution or utterance, complete with meaning, which he saw as comprising 'sense' and 'reference'.
the illocution --what we do WITH it.
the perlocution -- what we do BY it.
---
Since Grice's theory is psychologist (or as Alston prefers, 'ideational' -- in "Philosophy of Language"), Grice can always retreat to the idea that an allegedly vacuous names REFERS to the psychological content of the utterer:
"Euclid thought that Pegasus was a slow flyer".
This is an opaque context (that Grice considers briefly at the very end of "Vacuous Names"). Since we are allowed to use names (even vacuous) in opaque contexts like that, we should be always (note the reference to the infinity there) be ready to discuss "Pegasus", as used by Euclid, in terms of this or that belief on Euclid's part. "Pegasus" refers to the content of a belief by Euclid.
In
"As far as I know, there are infinitely many stars",
the issue may be more transparent (or not).
"By uttering "As far as I know, there are infinitely many stars", the utterer meant that as far as he knew, there were infinitely many stars.
I.e. if the utterer is myself,
I am expressing the belief that as far as I know there are infinitely many stars.
So there is a belief on my part that there are infinitely many stars.
So that the adjectival phrase, "infinitely many" belongs in the content of one of my beliefs.
Now comes the finitist cosmological sceptic,
"That's nonsense. Surely you cannot KNOW that there are infinitely many stars"
This can be interpreted variously:
As an actual negation: matter is finite. So, it is just FALSE that there are infinitely many stars. So A's belief contains a falsehood.
It can also be interpreted more metaphysically. It is just UNKNOWN whether there are infinitely many stars, so the opponet would be claiming that it is too bold to hold a belief about something unprovable.
This may relate to a point made by Jones on various occasions. If we take the statement,
"There are infinitely many stars" as METAPHYSICAL (and thus, according to the early logical positivists) as 'meaningless', then its negation tends also to the meaninglessness. Or not.
"tends to the meaninglessness" is my way of keeping track with the infinity, as in the famous (infamous) symbol,
--->
as used in different contexts.
----INTERLUDE from wikipedia http://en.wikipedia.org/wiki/Limit_of_a_function
Limits involving infinity

The limit of this function at infinity exists.
For
f(
x) a real function,
the limit of f as x approaches infinity is L, denoted

means that for all
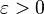
, there exists
c such that

whenever
x >
c. Or, symbolically:

Similarly,
the limit of f as x approaches negative infinity is L, denoted
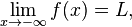
means that for all
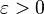
there exists
c such that

whenever
x <
c. Or, symbolically:

For example

Limits can also have infinite values.
When infinities are not considered legitimate values, which is standard (but see below), a formalist will insist upon various
circumlocutions.
For example, rather than say that a limit
is infinity, the
proper thing is to say that the function "diverges" or "grows without bound". In particular, the following informal example of how to pronounce the notation is arguably inappropriate in the classroom (or any other formal setting). In any case, for example
the limit of f as x approaches a is infinity, denoted

means that for all
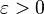
there exists
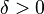
such that
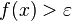
whenever

.
These ideas can be combined in a natural way to produce definitions for different combinations, such as

For example

Limits involving infinity are connected with the concept of
asymptotes.
These notions of a limit attempt to provide a metric space interpretation to limits at infinity.
However, note that these notions of a limit are consistent with the topological space definition of limit if
a neighborhood of −∞ is defined to contain an
interval [−∞,
c) for some
c ∈
R
a neighborhood of ∞ is defined to contain an interval (
c, ∞] where
c ∈
R
a neighborhood of
a∈
R is defined in the normal way metric space
R
In this case,
R is a topological space and any function of the form
f:
X →
Y with
X,
Y⊆
R is subject to the topological definition of a limit. Note that with this topological definition, it is easy to define infinite limits at finite points, which have not been defined above in the metric sense.
Many authors
[1] allow for the
real projective line to be used as a way to include infinite values as well as extended real line. With this notation, the extended real line is given as
R ∪ {-∞, +∞} and the projective real line is
R ∪ {∞} where a neighborhood of ∞ is a set of the form {
x: |
x|>
c}. The advantage is that one only needs 3 definitions for limits (left, right, and central) to cover all the cases.
As presented above, for a completely rigorous account, we would need to consider 15 separate cases for each combination of infinities (5 directions: -inf, left, central, right, and +inf; 3 bounds: -inf, finite, or +inf). There are also noteworthy pitfalls.
For example, when working with the extended real line,

does not possess a central limit (which is normal):

In contrast, when working with the projective real line, infinities (much like 0) are unsigned, so, the central limit
does exist in that context:

In fact there are a plethora of conflicting formal systems in use. In certain applications of
numerical differentiation and integration, it is, for example, convenient to have
signed zeroes.
A simple reason has to do with the converse of

, namely, it is convenient for

to be considered true.
Such zeroes can be seen as an approximation to
infinitesimals.
--- end of interlude.
Jones goes on:
"I'm afraid I
have lost my grip on the system since it is years since I did my rehash (see:
http://rbjones.com/rbjpub/pp/doc/t037.pdf)
so I would have to spend some time getting it back into my head before I could
see what the options are."
"Some time" sounds good to me. Or as I prefer, "take YOUR time" -- Cfr. the 'infinitesimal' (sic) use of time in popular song:
"Every TIME it rains it rains Pennies from Heaven".
---- This phrase, 'every time', surely does not commit the singer to infinity, but this below does:
Everybody loves a baby that's why I'm in love with you,Pretty baby, pretty baby,And I'd like to be your sister, brother, dad and mother too,Pretty baby, pretty baby.
- Won't you come and let me rock you in my cradle of love
- And we'll cuddle all the time.
- Oh, I want a lovin' baby, and it might as well be you,
- Pretty baby of mine,
- Pretty baby of mine.
Note the phrase,
"We'll cuddle all the time".
In symbols, this may IMPLICATE the infinity (or eternity). But I don't think so. Using a remark by Stanley (vide his contextualism), a finitist may intepret allegedly infinitist implicatures as being cancelled under a 'domain' or 'universe of discourse' -- so "all the time" does not read, as "all the time simpliciter" but as "all the time you and I are together" (or something). Note that however, this is implicatural and a TRANSFINITIST construal is always POETICALLY and plausibly possible.
---
Jones goes on:
"Meanwhile, Speranza has launched us into
extensionalism and other minimalisms (though perhaps he doesn't have more than
one) which are an important area in which one might imagine Grice to have
serious issue with Carnap, but in which I persist in thinking that Grice's does
not see all the possibilities and that not all notions of extensionalism and not
all practice of minimalism falls prey to his critiques, or ought by him to be
considered objectionable. So I am more inclined to chase this hare than get
deeper into how infinity might work for Grice, which probably does get very
complicated."
Indeed.
But before that, I will try to re-direct the other statements that Grice analyses in connection with the infinitely many stars.
Grice compares, in WoW, then
"So far as I know, there are infinitely many stars."
(How many?) (How can I _know_ 'infinite'? with a few other silly things (shall we say?) (silly?) people say:
"He is a lucky person."
"If "lucky" is understood, as it shouldn't, at least in Oxford, as a
'dispositional' adjective, the utterance turns out to be an alternative way of
saying the absurd claim:
"He is a person to whom what
is UNLIKELY to happen IS likely to happen".
A third example that Grice finds 'absurd, if ordinary' is:
"Departed spirits walk along this road
on their way to Paradise".
--- Grice comments:
"If this is being understood as meaning that departed
spirits _do_ walk, when they are, as the Anglican dogma goes, supposed to be
bodiless and imperceptible, then either the dogma is being openly
rejected, or the phrase meant _casually_."
A fourth and final example of ordinary absurdity cited by Grice is:
"I wish that I had been Napoleon."
("This," Grice notes, has to be distinguished from: "I wish I were LIKE
Napoleon". In this way, the utterance compares to: "I wish that I had lived
not in the XXth century, but in the XVIIIth century" -- another absurdity).
But yes, we should re-focus on minimalisms, extensionalisms, and possibilities that Grice may not find objectionable. Or not (i.e. that he MAY).
Talking of cashing the hare, I am reminded of the White professor of Moral Philosophy at Oxford:
R. M. Hare.
Oddly, there is an infinity connection with ethics (other than "you cannot run with the hare and chase with the hounds").
The philosopher Emmanuel Levinas uses "infinity", variously, and rather irritatingly (to a purist) to designate that which cannot be
defined or reduced to knowledge or power.
In Levinas' magnum opus Totality and
Infinity he says,
"Infinity [not of the Cantorian type] is produced in the relationship of the same
with the other, and how the particular and the personal, which are
unsurpassable, as it were magnetize the very field in which the production of
infinity is enacted."
"The idea of infinity is not an incidental notion
forged by a subjectivity to reflect the case of an entity encountering on the
outside nothing that limits it, overflowing every limit, and thereby infinite."
"The production of the infinite entity is inseparable from the idea of infinity,
for it is precisely in the disproportion between the idea of infinity and the
infinity of which it is the idea that this exceeding of limits is produced."
"The
idea of infinity is the mode of being, the infinition, of infinity."
"All
knowing qua intentionality already presupposes the idea of infinity, which is
preeminently non-adequation."
— p. 26-27
This relates to Wittgenstein. And we may explore this as we reconsider usual phrases in ordinary language that seem to IMPLICATE the infinite. In a few quotes unreferenced to Witters in Wikipedia, we read:
Modern philosophical views[edit]
Modern discussion of the infinite is now regarded as part of set theory and mathematics. This discussion is generally avoided by philosophers. An exception was
Wittgenstein, who made an impassioned attack upon
axiomatic set theory, and upon the idea of the actual infinite, during his "middle period".
[1]
Does the relation  correlate the class of all numbers with one of its subclasses? No. It correlates any arbitrary number with another, and in that way we arrive at infinitely many pairs of classes, of which one is correlated with the other, but which are never related as class and subclass. Neither is this infinite process itself in some sense or other such a pair of classes... In the superstition that
correlate the class of all numbers with one of its subclasses? No. It correlates any arbitrary number with another, and in that way we arrive at infinitely many pairs of classes, of which one is correlated with the other, but which are never related as class and subclass. Neither is this infinite process itself in some sense or other such a pair of classes... In the superstition that  correlates a class with its subclass, we merely have yet another case of ambiguous grammar.
correlates a class with its subclass, we merely have yet another case of ambiguous grammar.
— Philosophical Remarks § 141, cf Philosophical Grammar p. 465
Unlike the traditional empiricists, he thought that the infinite was in some way given to
sense experience.
... I can see in space the possibility of any finite experience... we recognise [the] essential infinity of space in its smallest part." "[Time] is infinite in the same sense as the three-dimensional space of sight and movement is infinite, even if in fact I can only see as far as the walls of my room.
... what is infinite about endlessness is only the endlessness itself.
The two later quotes are especially interesting. The very last, in its obscurity. The other in its implicature.
More later, I hope.
-----
and then there's one half of Grice's favourite philosopher, Kantotle.
Kant ends the
second Critique on a hopeful note about the future of ethics.
The wonders of
both the physical and the ethical worlds are not far for us to find.
To feel
awe, we should only look upward to the infinitely many stars or inward to the moral law which
we carry around within us.
The study of the physical world was dormant for
centuries and wrapped in superstition before the physical sciences actually
came into existence.
We are allowed to hope that soon the moral sciences will
replace superstition with knowledge about ethics.
--
Posted
By Blogger to
The
Grice Club at 6/19/2013 01:55:00 AM



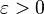 , there exists c such that
, there exists c such that  whenever x > c. Or, symbolically:
whenever x > c. Or, symbolically:
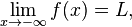



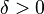 such that
such that 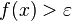 whenever
whenever  .
.

 does not possess a central limit (which is normal):
does not possess a central limit (which is normal):

 , namely, it is convenient for
, namely, it is convenient for  to be considered true.
to be considered true.  correlate the class of all numbers with one of its subclasses? No. It correlates any arbitrary number with another, and in that way we arrive at infinitely many pairs of classes, of which one is correlated with the other, but which are never related as class and subclass. Neither is this infinite process itself in some sense or other such a pair of classes... In the superstition that
correlate the class of all numbers with one of its subclasses? No. It correlates any arbitrary number with another, and in that way we arrive at infinitely many pairs of classes, of which one is correlated with the other, but which are never related as class and subclass. Neither is this infinite process itself in some sense or other such a pair of classes... In the superstition that 

